¿Qué es baricentro?

Definición de baricentro

La definición correspondiente a este término, dentro de la Física es: el centro de gravedad de un cuerpo. Coincide con el centro de masas del cuerpo en el caso en que su densidad sea uniforme u homogénea o cuando la materia se distribuye según algunas propiedades específicas tales como la simetría.

Por extensión también se llama de esta manera al punto de aplicación que resulta de un sistema de fuerzas.

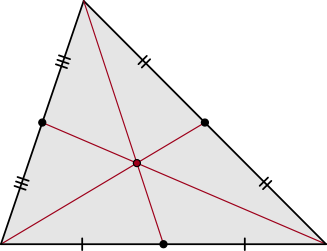
En Geometría se conoce con esta denominación al punto de intersección que se forma con las medianas de un triángulo. Definiendo a las medianas como la recta que une el punto medio del lado de un triángulo con el vértice opuesto. Llamado también centroide, se lo formula con la letra G.

A su vez, cada mediana es dividida en dos segmentos, comprobándose que el segmento que une el vértice con el baricentro tiene como medida el doble de la que lo une con el punto medio del lado opuesto.

De este modo este centroide es el centro de simetría de una figura geométrica, que también se lo define como un punto fijo del grupo de isometría de esa figura.

Sus propiedades algebraicas son:

*asociatividad ya que se puede calcular por puntos reagrupados, o sea introduciendo baricentros parciales.

*homogeneidad, eso es que si se multiplican todas las masas por un mismo coeficiente k ≠ 0, este punto no cambia.

En el caso de un tetraedro, si se quiere fijar a este centroide, el mismo se halla en el punto donde se cortan los segmentos que unen el isobaricentro de una cara con el vértice opuesto.

Para poder calcular el baricentro geométricamente en un polígono tanto regular como irregular existe una forma sencilla y práctica:

-los elementos geométricos que deben utilizarse son regla y compás.

-se parte de un polígono de n vértices.

-se descompone ese polígono en cuadriláteros y triángulos que no posean vértices en común, es decir, que sean disjuntos.

-se calculan los baricentros de estos cuadriláteros y triángulos y luego formar el polígono.

-se puede comprobar que este algoritmo tiene un orden de logaritmo.

-finalmente se vuelve al primer paso.

Ejemplos de uso y frases

“El estudiante ha realizado el cálculo del baricentro de una figura tetraédrica con suma rapidez”. En este ejemplo, se usa aplicándose a un cuerpo geométrico.

“Ha trazado las medianas del triángulo y ha fijado como G su baricentro”. Se refiere en este caso, a la intersección de esos segmentos.

“En este examen le han pedido que demuestre las propiedades del baricentro de una figura geométrica dada”. Aquí, se utiliza con referencia a una demostración práctica.