¿Qué es productos notables?
Definición 
Sinónimos 
Ejemplos de uso 
Los productos notables se utilizan en matemáticas, específicamente en álgebra, y cuya característica es que son productos cuyo resultado se obtiene sin tener que realizar la operación de multiplicar, sino conociendo ciertas reglas fijas.
Clase: construcción sustantiva formada por un sustantivo masculino plural (productos) y un adjetivo masculino/femenino, plural (notables).
Definición de productos notables
La definición de productos notables es la expresión algebraica que se puede factorizar a simple vista, sin tener que realizar la operación.
Dicho de otra manera se puede decir que son productos cuyo resultado se obtiene sin que se necesite efectuar la multiplicación, solamente con aprender su desarrollo, se llega al resultado.
Algunos de estos productos notables son:
1-Binomio al cuadrado o cuadrado de la suma de dos cantidades:
(expresión algebraica) a2 + 2ab + b2 = (a + b)2 (producto notable)
De este modo el cuadrado de la suma de dos cantidades es equivalente a la primera cantidad al cuadrado; más el doble de la primera cantidad multiplicada por la segunda, sumada a la segunda cantidad al cuadrado.
Esto significa que cuando se tiene una expresión como a2 + 2ab + b2 se sabe que se la puede factorizar en (a + b)2
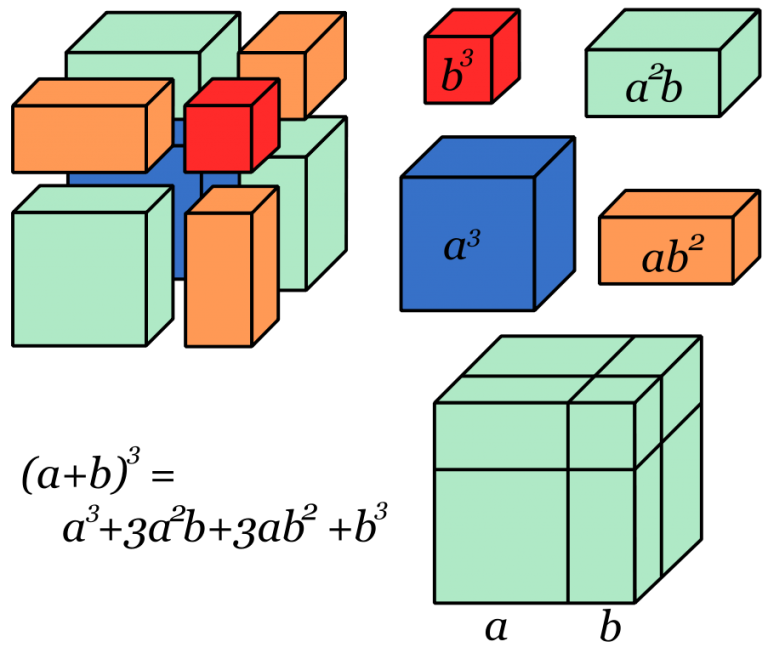
2-Binomio al cubo
Esto implica que el cubo de la primera cantidad más el cubo de la segunda cantidad es igual al cubo de la primera; más el triple de la primera cantidad al cuadrado por la segunda; sumado el triple de la primera cantidad por la segunda al cuadrado; más la segunda al cubo.
De este modo cuando se tiene la expresión a3 + 3a2b + 3ab2 + b3 se puede factorizar en (a + b)3
3-Diferencia de cuadrados o cuadrado de la diferencia de dos cantidades
El cuadrado de la diferencia de dos cantidades es igual a la primera cantidad al cuadrado menos la multiplicación del doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda.
Así es que cuando aparece la siguiente expresión: a2 – 2ab + b2, se la puede factorizar en el siguiente producto notable (a – b)2
4-La suma de dos números por su diferencia (a + b) (a – b) es igual a la diferencia del cuadrado del primer término menos el cuadrado del segundo.
De este modo cuando aparece la antedicha expresión algebraica se puede resolver a través del producto notable: a2 – b2
5-Trinomio al cuadrado
El cuadrado de la suma de tres cantidades es equivalente al cuadrado de la primera cantidad, más el cuadrado de la segunda, más el cuadrado de la tercera, más el doble del producto de la primera por la segunda; más el doble del producto de la primera por la tercera; más el doble del producto de la segunda por la tercera.
Así si se tiene la siguiente expresión algebraica:
a2 + b2 + c2 + 2ab + 2ac + 2bc se puede factorizar en el producto notable (a + b + c)2
Con referencia a la etimología de la construcción, ambas palabras provienen del latín:
“Producto” proviene de productus, producta, productum participio del verbo produco, producis, producere, produxi, productum. Verbo formado por el prefijo pro- cuyo significado es delante, en adelante, a la vista, a favor y por el verbo duco, ducis, ducere, duxi, ductum con el significado de hacer, llevar hacia, guiar, conducir.
“Notable” deriva de notabilis, notabile cuyo concepto es notable, señalado.
Sinónimos de productos notables
Productos especiales.
Ejemplos de uso y frases
“En su blog, el profesor ejemplificó todos los casos de productos notables para sus alumnos”. Se refiere en este caso a su enseñanza.
“Por no saber resolver los productos notables reprobó el examen”. Aquí, se aplica a una prueba escolar.
“Cuando le hablaron de productos notables pensó en objetos valiosos jamás imaginó que se trataba de expresiones algebraicas”. En esta oración, se usa con el sentido de desconocimiento del significado matemático.
