¿Qué es topología?
La topología es una especialización que se encarga del estudio de las características y propiedades que tienen los cuerpos geométricos y que no se alteran debido a cambios continuos, independientemente de su apariencia o tamaño.
Clase: sustantivo, femenino, singular.
Definición de topología
La definición de este término es una parte de las matemáticas que estudia las propiedades que permanecen inalteradas por transformaciones continuas en los cuerpos geométricos.
Entre los conceptos que aborda esta disciplina están los de números de agujeros, proximidad, textura que tiene un objeto, así como también la comparación entre objetos y la clasificación de propiedades tales como metricidad, conectividad, entre otras.
Además de utilizarse este término en un sentido informal en las matemáticas, también se lo usa de manera formal. En ese sentido se refiere a un grupo de subconjuntos de un conjunto determinado, grupo o también llamado familia que cumple con las propiedades de intersección y unión.
Para entender su funcionamiento hay que saber que para la topología, dos objetos son equivalentes en tanto tengan el mismo número de huecos, intersecciones, pedazos, etc. También hay que saber que en esta ciencia está permitido estirar, encoger, retorcer, doblar los objetos, siempre y cuando no se rompa ni se separe lo que ya estaba unido, ni unir lo que estaba separado. Por ejemplo una esfera es topológicamente equivalente a un cubo, porque, sin que se rompan, cada uno se puede deformar en continuidad hasta poder coincidir en el otro. Por el contrario, una esfera no es equivalente de ese modo a la forma geométrica de un neumático de automóvil, ya que la esfera debería romperse para formar el agujero central.
Por lo anteriormente expuesto es que se conoce a esta disciplina como la “geometría de la página de goma”, porque en realidad es como se estuviera estudiando geometría sobre una lámina de goma que se pudiera encoger, estirar, etc.
Habitualmente se suele considerar como el inicio de esta disciplina en 1735, con la resolución de Euler para el problema de los puentes de Königsberg. Aunque sus antecedentes se remontan a Euclides en el 300 a.C. cuando estudia los poliedros regulares.
Luego de Euler, se pueden destacar los trabajos de Möbius y Listing descubren la banda de Möbius, en 1858.
Posteriormente Giuseppe Peano, en 1890, demuestra que un cuadrado que se rellena también es una curva. Y en la década de 1920 Urysón y Menger definen el concepto de curva a partir de esta ciencia.
La topología se suele dividir en 3 ramas:
-algebraica
-diferencial
-general.
Pero también existen elementos topológicos en otras disciplinas de las matemáticas tales como la teoría de nudos, de la medida, o el análisis funcional.
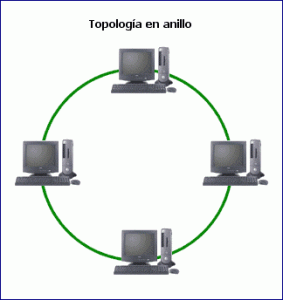
Asimismo se llama topología de red a un mapa físico o lógico de una red que sirve para intercambiar datos. De acuerdo con esto se debe entender como la manera en que se ha diseñado una red física como lógicamente.
En cuanto al origen de topología está formada a partir de raíces del griego. En primer lugar topo- que proviene de τοπος, τοπου (pr.topos, topu) cuyo significado es lugar, país, paisaje, espacio, territorio y por otra, logía que procede del sustantivo λογία (pr. logía) (ver cronología).
Ejemplos de uso y frases
“Está realizando una clasificación de topologías de redes para presentar en un trabajo en la universidad”. Se refiere en este caso, a un trabajo práctico.
“Para la topología una taza puede transformarse en una rosquilla”. En esta oración, se usa con el sentido de un ejemplo.
“Está estudiando topología molecular mediante la cual describe algebraicamente los compuestos químicos”. Aquí, se aplica a la química matemática.
 Definición
Definición  Ejemplos de uso
Ejemplos de uso