¿Qué es distancia entre dos puntos?
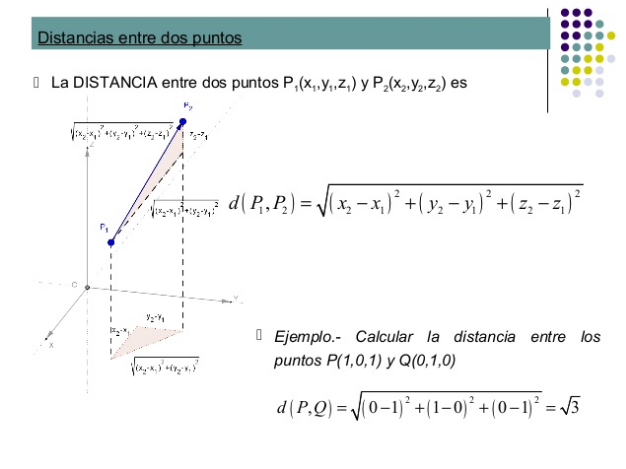
La distancia entre dos puntos está vinculada al plano cartesiano, ya que este permite calcular la distancia que existe entre ambos puntos, a partir de la ubicación de las coordenadas de ambos.
Por su parte, cuando ambos puntos pasan del plano a la superficie terrestre, su distancia se calcula de otra manera. De acuerdo con la metodología denominada fórmula del Haversine.
Clase: construcción sustantiva formada por un sustantivo femenino singular (distancia); una preposición (entre); un adjetivo numeral (dos) y un sustantivo masculino plural (puntos).
Definición de distancia entre dos puntos
La definición de distancia entre dos puntos es la recta imaginaria que los une en el espacio, marcando el menor trayecto entre ambos. Esto puede darse también en el plano cartesiano o simplemente sobre la superficie terrestre. De acuerdo a cada caso, su cálculo es diferente.
Con referencia al plano cartesiano, el mismo se utiliza como un sistema de referencia para ubicar puntos en un plano. Y es a través de la ubicación de las coordenadas de dos puntos, que se puede calcular justamente la distancia entre ellos.
De manera que cuando los dos puntos:
–se hallan sobre el eje x (correspondiente a las abscisas) o en una recta paralela a este eje, la distancia es el valor absoluto de la diferencia de sus abscisas (x2 – x1)
-se hallan sobre el eje y (de las ordenadas) o en una recta que está paralela a dicho eje. En tanto la distancia es el valor absoluto de la diferencia de sus ordenadas (y1 – y2).
Si los puntos se hallan en cualquier otro lugar del sistema de coordenadas, la distancia entonces, queda establecida por la relación:
Otra manera de calcularla es aplicando el Teorema de Pitágoras cuya fórmula es: a2 + b2 = c2. Su enunciado es. En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Para esto se debe ubicar cada punto en su respectiva coordenada por ejemplo: P1 (x1, y1 y P2 (x2, y2) y luego formar un triángulo rectángulo de hipotenusa P1 P2 y allí aplicar el teorema.
En cuanto al cálculo de la distancia entre dos puntos terrestres, se calcula por la fórmula del Haversine o del semiverseno que es una ecuación astronómica que permite calcular la distancia de círculo máximo entre dos puntos del globo terráqueo sabiendo su longitud y su latitud. A través de esta ley de seversenos se relacionan los lados y ángulos de los triángulos esféricos.
En cuanto al origen etimológico de esta construcción, todas sus palabras provienen del latín:
“Distancia” deriva de distantia, distantiae, sustantivo que se forma a partir de distans, distantis. Este es el participio presente del verbo disto, distas, distare cuyo significado es estar alejado, distar. Verbo constituido por el prefijo dis- que señala divergencia, separación múltiple. Al que se le suma el verbo sto, stas, stare, steti, statum que significa estar de pie, estar inmóvil. Por su parte, a la base se le suma el sufijo -nt- que señala al agente más el sufijo -ia que indica cualidad.
“Entre” surge de la preposición inter.
“Dos” deriva del numeral duo, duae, duo
“Punto” nace de punctum, puncti, sustantivo que proviene de punctus, puncta, punctum. Este es el participio del verbo pungo, pungis, pungere, pupugi, punctum con el concepto de picar, punzar.
Ejemplos de uso y frases
“Está aplicando la fórmula de distancia entre dos puntos que le han dado para aplicar en el plano cartesiano”. Se refiere en este caso, al uso de la fórmula en el plano.
“En la actualidad la distancia entre dos puntos terrestres se puede saber simplemente utilizando determinados programas en internet como Google maps o MySql”. En este ejemplo, se usa con el sentido de cálculos de distancia de puntos terrestres.
“Como quiere hacerlo rápido y bien va a aplicar el Teorema de Pitágoras para calcular la distancia entre dos puntos”. Aquí, se aplica refiriéndose a otra manera de calcularla.
 Definición
Definición  Ejemplos de uso
Ejemplos de uso 












