¿Qué es factorial?
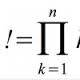
La palabra factorial se forma a partir de factor y este proviene del latín. Deriva del supino (factum) del verbo facio, facis, facere, feci, factum con el significado de hacer; más el sufijo -or que indica agente. A esa base se le añade el sufijo -alis que indica relación o pertenencia.
En consecuencia el concepto original de este es lo perteneciente o lo relativo al que hace.
Clase: adjetivo, por terminar en -l, su género es neutro o invariable ya que se puede utilizar tanto para el masculino como para el femenino, singular.
Definición de factorial
Su definición es el producto de todos los términos de una progresión aritmética.
También es el producto de todos los números naturales enteros positivos desde 1 hasta n. A este entero positivo se lo denomina el factorial de n.
De este modo para todo entero natural n, se denomina factorial de n al producto de todos los números enteros entre 1 y n: n! = 1 x 2 x 3 x … x (n-1) x n se impone 0! = 1, con el fin de que la relación n! = n x (n -1)! Sea válida asimismo par n=1.
Con esa relación se los pueden definir por inducción. De este modo los primeros son:
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320 y así sucesivamente.
El factorial de n: n! fue utilizado por primera vez por Christian Kramp, en 1803. Este matemático francés nació en Alsacia el 8 de julio de 1760 y murió en Estrasburgo 1826. Se inicia como profesional en medicina, pero luego de publicar libros sobre ella, empieza a interesarse en otras ciencias, tales como la cristalografía.
Cuando Francia anexa Renania, Kramp deja la medicina y comienza a enseñar Física, Química y Matemáticas en Colonia. Luego fue profesor en Renania y luego, en 1817 enseñó Geometría en la Academia de Ciencias. Fue en ese lugar que comenzó a trabajar en el factorial de n para números enteros junto a Gaus, Legendre y Bessel. Los resultados fueron independientes de los que por otro lado realizaban Stirling y Vandermonde.
La fórmula propuesta por Kramp ha sido:
Donde la pi mayúscula se llama productorio y es un operador matemático que representa una multiplicación de una serie de números infinita o finita.
Sus usos dentro de las matemáticas son muchos, pero sobre todo se utilizan en permutaciones y combinaciones.
Ejemplos de uso y frases
“El método de una función factorial se considera iterativo porque efectúa un recorrido o iteración por los diferentes números, multiplicando en cada paso el número siguiente de la serie por el siguiente que es el anterior más 1”. Se refiere en este caso, al cálculo de esta función.
“Se ha comprado una calculadora científica porque con ella puede conocer la función factorial”. En este ejemplo, se usa con el sentido de una calculadora con esta función.
“El profesor explicó que así como existe un función factorial existe, por definición, una función recursiva de la anterior”. Aquí, se aplica a dos funciones opuestas.
 Definición
Definición  Ejemplos de uso
Ejemplos de uso